Υπάρχει κάποιο όριο στο μέγεθος του πλαισίου στο οποίο μπορεί να θεωρηθεί ότι υπάρχουν κβαντικές υπερθέσεις;

Η καθημερινή εμπειρία μας δείχνει ότι τα «μεγάλα» σώματα δεν φαίνεται να υπάρχουν σε υπέρθεση καταστάσεων, όπως είναι δυνατό για τα περισσότερα κβαντικά σωμάτια, όπως τα ηλεκτρόνια. Μήπως αυτό σημαίνει ότι η κβαντική φυσική, ουσιαστικά δεν εφαρμόζεται σε αντικείμενα πέρα από ένα ορισμένο μέγεθος;

Ένα νέο πείραμα, που επιτρέπει να παρακολουθείται η κίνηση ενός μεγάλου ατόμου σε ένα οπτικό πλέγμα, θα μπορούσε να βοηθήσει στην έρευνα για το ποια είναι αυτή η οριακή τιμή. Χρησιμοποιώντας το πλαίσιο αυτό, ο Carsten Robens στο Πανεπιστήμιο της Βόννης, στη Γερμανία και οι συνάδελφοί του, έδειξαν ότι ένα άτομο καισίου ταξιδεύει κατά ένα πραγματικά μη-κλασικό τρόπο, κινούμενο ως μια κβαντική υπέρθεση καταστάσεων και έτσι καταλαμβάνοντας περισσότερες από μια διακριτές θέσεις την ίδια στιγμή.

Μεγαλύτερα αντικείμενα παρατηρήθηκαν να έχουν τέτοιες εγγενώς κβαντικές ιδιότητες, αλλά η παρατήρηση του Robens και των συνεργατών του βασίζεται σε ένα αυστηρό έλεγχο, που θεωρείται ως ο χρυσός κανόνας για την επιβεβαίωση, ότι υπάρχει υπέρθεση. Ως εκ τούτου, το πείραμά τους περιορίζει θεωρίες της φυσικής που στοχεύουν να αντικαταστήσουν τη κβαντική μηχανική. Η τεχνική τους θα μπορούσε επίσης να χρησιμοποιηθεί για να ελεγχθούν οι υπερθέσεις σε όλο και περισσότερες μακροσκοπικές κλίμακες, όπως με μεγάλα άτομα ή μόρια.

Τα περισσότερα πειράματα στοχεύουν να επιβεβαιώσουν ότι ένα σωμάτιο είναι σε κβαντική υπέρθεση καταστάσεων ερευνώντας για στοιχεία συμβολής. Το κλασικό πείραμα είναι η διέλευση ενός ηλεκτρονίου δια μέσου δυο σχισμών. Η κροσσοί που παράγονται υποδηλώνουν την κυματική συμπεριφορά που η κβαντική θεωρία αποδίδει στα θεμελιώδη σωμάτια. Ακόμη και αν αυτά τα πειράματα συμφωνούν με αυτό που η θεωρία προβλέπει, δεν είναι ασφαλή τεστ, επειδή είναι πιθανή μια κλασική εξήγηση: μπορεί κάποιος να φανταστεί ότι το ηλεκτρόνιο στην πραγματικότητα περνάει μέσα από τη μια σχισμή ή την άλλη και ποτέ διαμέσου και των δυο ταυτόχρονα (όπως θέλει η κβαντική φυσική).

Οι Anthony Leggett και Anupam Garg, σε μια θεωρητική μελέτη, το 1985, προσέγγισε το πρόβλημα εντελώς διαφορετικά. Αντί για έρευνα επιβεβαίωσης της κβαντικής θεωρίας, η μελέτη πρότεινε ότι θα πρέπει, αντί να προσπαθεί κάποιος να αποκλείσει τις εναλλακτικές, να δείξει ότι οτιδήποτε άλλο, εκτός από μια κβαντική περιγραφή, οδηγεί σε αντίφαση με την πειραματική παρατήρηση. Προσδιόρισαν μια άποψη που ονομάστηκε «μακρορεαλισμός», που βασίζεται σε δυο παραδοχές σε σύγκρουση με την κβαντική θεωρία: ένα αντικείμενο μεγάλου μεγέθους βρίσκεται πάντα σε μια θέση σε μια στιγμή (δεν υπάρχουν μακροσκοπικές υπερθέσεις) και η θέση του σώματος μπορεί να προσδιοριστεί χωρίς να διαταραχθεί. Έδειξαν ότι αν ο «μακρορεαλισμός» ήταν αλήθεια, μετρήσεις που εκτελούνται σε διαφορετικές στιγμές σε ένα αντικείμενο, θα μπορούσαν μόνο να συσχετίζεται στατιστικά έως ένα ορισμένο βαθμό, μια συσχέτηση που εκφράζεται μαθηματικά με την ανισότητα Leggett-Garg. Πειράματα που δείχνουν διαφορετικά, δηλαδή ότι αυτή η ανισότητα παραβιάζεται, θα έδειχναν ότι ο «μακρορεαλισμός» είναι σαφώς ψευδής. Η εργασία τους ενέπνευσε μια σειρά από πειράματα σε φωτόνια, πυρηνικά spins και υπεραγώγιμα κυκλώματα.

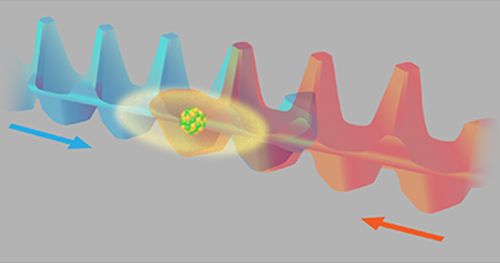
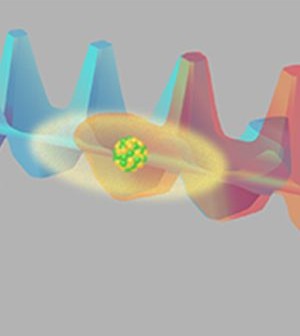
Στο πείραμα ελέγχου του Robens και των συνεργατών του, ένα μεγάλο άτομο (κέσιο) κινείται σε ένα από δυο δυνατά οπτικά πεδία, στην εικόνα δείχνονται ως κόκκινο και μπλε. Τα πεδία έχουν περιοδικό δυναμικό με μορφή που μοιάζει με τομή μιας χαρτονένιας αυγοθήκης.

Σε σύγκριση με τα προηγούμενα πειράματα, τα άτομα που μελετήθηκαν στα πειράματα του Robens και των συνεργατών του, είναι τα μεγαλύτερα κβαντικά αντικείμενα με τα οποία δοκιμάστηκε η ανισότητα Leggett-Garg, με τη χρήση αυτού που αποκαλείται «μηδενική μέτρηση»-μια «μη-επεμβατική» μέτρηση, που επιτρέπει την ανισότητα να επιβεβαιώνεται με τον δυνατότερο βολικό τρόπο.

Στο πείραμα των ερευνητών, ένα άτομο καισίου κινείται σε ένα από δυο οπτικά στάσιμα κύματα, τα οποία έχουν αντίθετη πόλωση ηλεκτρικού πεδίου και η θέση του ατόμου μετριέται σε διαφορετικούς χρόνους. Τα δυο στάσιμα κύματα μπορούν να απεικονιστούν ως μικρό ζευγάρι επικαλυπτόμενων μονοδιάστατων (σχήματος όμοιου με αυτό τομής χάρτινων αυγοθηκών) λωρίδων-μιας κόκκινης και μιας μπλε (όπως φαίνεται στην εικόνα). Το πείραμα συνίσταται στη μέτρηση συσχετισμού μεταξύ της θέσης του ατόμου σε διάφορους χρόνους. Ο Robens και οι συνεργάτες του, πρώτα έθεσαν το άτομο σε υπέρθεση των δυο εσωτερικών υπέρλεπτων καταστάσεων του spin. Αυτό αντιστοιχεί στο να βρίσκεται ταυτόχρονα σε δυο χαρτόκουτα. Στη συνέχεια, η ομάδα δημιούργησε ολίσθηση των δυο οπτικών κυμάτων, το ένα μέσα από το άλλο, που έγινε αιτία να απλωθεί το άτομο επάνω σε μια απόσταση περίπου 2 μικρομέτρων, σε μια κίνηση γνωστή ως «κβαντικό βάδισμα». Τέλος, οι συγγραφείς διέγειραν οπτικά το άτομο, προκαλώντας το φθορισμό και να αποκαλύψει τη θέση του σε ένα μόνο τόπο.

Γνωρίζοντας από που ξεκίνησε το άτομο, τους επέτρεψε να υπολογίσουν , κατά μέσο όρο, αν το άτομο κινήθηκε αριστερά ή δεξιά από τη θέση εκκίνησης. Επαναλαμβάνοντας το πείραμα, μπόρεσαν να πάρουν συσχετισμούς μεταξύ της θέσης του ατόμου σε διαφορετικές στιγμές, που εισήγαγαν στην ανισότητα Leggett-Garg. Τώρα, μια «μακρορεαλιστική» θεώρηση θα μπορούσε να ισχυριστεί ότι το άτομο δεν άρχισε ποτέ σε μια υπέρθεση. Μάλλον σε κάθε δεδομένη στιγμή βρισκόταν στον κάδο του ενός χαρτόκουτου ή του άλλου. Επιπλέον θα μπορούσε να υποστηρίξει ότι μια μέτρηση φθορισμού ήταν επεμβατική σε επόμενες μετρήσεις. Ως εκ τούτου, όπως αρχικά είχαν προτείνει οι Leggett και Garg, ο Robens και οι συνεργάτες του, χρησιμοποίησαν την τεχνική μέτρησης «μηδενικού αποτελέσματος» σε μια από τις ενδιάμεσες χρονικές στιγμές στο πείραμά τους. Με απλά λόγια, μια «μηδενική μέτρηση» επιτρέπει τον πειραματιστή να προσδιορίσει τη θέση του ατόμου χωρίς να αλληλεπιδράσει απευθείας με αυτό.

Για να το πετύχουν αυτό, οι συγγραφείς, απλά μετατόπισαν ένα από τα στάσιμα κύματα-ή χαρτόκουτα-σε μια μακρινή απόσταση. Ας πούμε ότι μετακίνησαν το κόκκινο χαρτόκουτο μακριά. Αν το άτομο αποτυγχάνει να λάμψει, όταν αργότερα εκτελείται μια μέτρηση φθορισμού, γνωρίζει κάποιος ότι το άτομο ήταν στο κόκκινο χαρτόκουτο, αλληλεπιδρούσε ισχυρά με αυτό και κατέληξε μακριά. Επαναλαμβάνοντας το πείραμα, ωστόσο, μερικές φορές βρίσκει κανείς το άτομο να λάμπει. Μπορεί, τότε, κάποιος να είναι σίγουρος ότι το άτομο ήταν στο μπλε χαρτόκουτο πριν από την μετακίνηση, όταν ενεργοποιήθηκε η μέτρηση. Επιπλέον γνωρίζει κάποιος ότι το μπλε χαρτόκουτο και έτσι το άτομο κεσίου, δεν αλλοιώθηκε.

Αν ο «μακρορεαλισμός» περιέγραφε την πραγματικότητα, μια μηδενική μέτρηση δεν θα επηρέαζε την έκβαση της τελικής μέτρησης φθορισμού και η συνολική συσχέτιση της θέσης του ατόμου σε διάφορες χρονικές στιγμές, θα μπορούσε να είναι κατανοήσιμη χωρίς την κβαντομηχανική. Αλλά αυτό χτυπά στην καρδιά αυτού που κάνει την κβαντομηχανική τόσο παράξενη. Κυρίως όταν το άτομο απλώνεται, σε αντίθεση με το να έχει μια ορισμένη θέση, ακόμη οι μηδενικές μετρήσεις έχουν ένα αποτέλεσμα. Αυτό το άπλωμα οδηγεί σε μια ισχυρότερη ολική συσχέτιση, από ότι είναι δυνατό στο πλαίσιο του «μακρορεαλισμού», γεγονός που μαθηματικά συλλαμβάνεται με μια παραβίαση της ανισότητας Leggett-Garg.

Αυτό είναι ακριβώς που βρήκαν ο Robens και οι συνεργάτες του και αυτό σημαίνει ότι ο «μακρορεαλισμός» δεν μπορεί να εφαρμοστεί στο (δικό τους) άτομο καισίου. Ένα αιώνα, σχεδόν, μετά την κβαντική επανάσταση στην επιστήμη, ίσως εκπλήσσει το γεγονός ότι οι φυσικοί ακόμη προσπαθούν να αποδείξουν την ύπαρξη των υπερθέσεων. Το πραγματικό κίνητρο βρίσκεται στο μέλλον της θεωρητικής φυσικής. Οι νεοπαγείς θεωρίες του «μακρορεαλισμού» μπορεί κάλλιστα να διαμορφώσουν τη βάση της επόμενης γενιάς «αναβάθμισης» της κβαντικής φυσικής θέτοντας την κλίμακα του συνόρου κβαντικής και κλασσικής προσέγγισης. Χάρη στα αποτελέσματα αυτού του πειράματος, μπορούμε να είμαστε σίγουροι ότι το σύνορο δεν μπορεί να βρίσκεται στην κλίμακα στην οποία το άτομο του κεσίου φαίνεται να συμπεριφέρεται ως κύμα.

Πόσο υψηλή είναι αυτή η κλίμακα; Μια θεωρητική μέτρηση της μακροσκοπικότητας δίνει στο άτομο του κεσίου μια μέτρια κατάταξη της τάξης του 6,8, επάνω από το μόνο άλλο αντικείμενο που ελέγχθηκε με μηδενική μέτρηση, αλλά πολύ κάτω από εκεί που οι περισσότεροι υποψιάζονται ότι βρίσκεται το όριο. Στην πραγματικότητα πειράματα συμβολομετρίας υλικών κυμάτων έχουν ήδη δείξει κροσούς συμβολής μορίων φουλαρενίων, τοποθετώντας τα σε μια κατάταξη τόσο υψηλή όσο το 12. Πάντως θεωρείται ότι μπορούμε να είμαστε σίγουροι για την επίδειξη της κβαντικότητας του ατόμου του καισίου, λόγω του αποκλεισμού από τους συγγραφείς του «μακρορεαλισμού» μέσω των μετρήσεων μηδενικού αποτελέσματος. Το επόμενο βήμα είναι να πραγματοποιηθούν τέτοια πειράματα με μεγαλύτερες μάζες, με υπερθέσεις για μεγαλύτερες χρονικές κλίμακες και χωρισμένες σε μεγαλύτερες αποστάσεις. Αυτό θα ωθήσει την περιοχή της μακροσκοπικότητας παραπέρα και θα αποκαλύψει ακόμη περισσότερα σχετικά με τη φύση των σχέσεων της κβαντικής και του μακρόκοσμου.

Πηγή: Άρθρο του George Knee στην APS

Περισσότερα στο άρθρο: Ideal Negative Measurements in Quantum Walks Disprove Theories Based on Classical Trajectories, στο Physical Review X (2015).