Φυσική Συμπυκνωμένης Ύλης: Όταν μια τετραγωνική ρίζα ενός πλέγματος οδηγεί σε τοπολογικές καταστάσεις

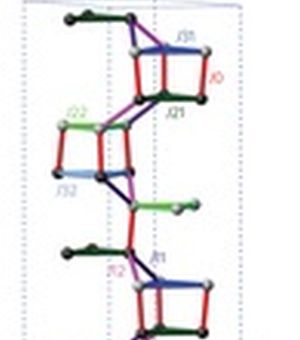
Πώς σχεδιάζεις ένα τοπολογικό υλικό από την αρχή; Αυτό είναι ένα ερώτημα που οι ερευνητές θέτουν με ένταση αυτές τις ημέρες, καθώς εστιάζουν στο χτίσιμο πλεγμάτων για ηλεκτρόνια, άτομα, φως και ήχο που, λόγω της συμμετρίας του πλέγματος, φιλοξενούν καταστάσεις που είναι απρόσβλητες από διαταραχές. Ο Jake Arkinstall του Πανεπιστημίου του Lancaster, στο Ηνωμένο Βασίλειο, και οι συνάδελφοί του δίνουν μια απάντησή: αρχίζουν με ένα κανονικό κρυσταλλικό πλέγμα και μετά βγάζουν την τετραγωνική ρίζα της κβαντομηχανικής εξίσωσης που το περιγράφει. Σε ορισμένες περιπτώσεις, η λύση της νέας εξίσωσης θα περιγράφει ένα πλέγμα με τοπολογικές καταστάσεις. Και αντίθετα από άλλες συνταγές για τη μηχανική τοπολογικών υλικών, αυτή δεν εισάγει νέα συστατικά – τα στοιχεία στο «γονεϊκό» πλέγμα και στο «παιδί», που παράγεται από την τετραγωνική ρίζα του «γονέα», είναι τα ίδια, είναι μόνο οι συζεύξεις μεταξύ των στοιχείων που αλλάζουν.

Η προσέγγιση της ομάδας έχει ένα γνωστό προηγούμενο: Στη δεκαετία του 1920, ο Dirac ανακάλυψε το ποζιτρόνιο όταν έβγαλε την τετραγωνική ρίζα της εξίσωσης Klein-Gordon για σχετικιστικά σωμάτια. Ο Arkinstall και ο συνάδελφοί του μετέφεραν αυτή την ιδέα στα αποκαλούμενα μοντέλα ισχυρής δέσμευσης, τα οποία συχνά χρησιμοποιούνται για να υπολογίσουν τις ενεργειακές ζώνες για τα ηλεκτρόνια σε στερεά ή στο φως σε μια συστοιχία κυματοδηγών. Πρώτα, θεώρησαν ένα αντιπροσωπευτικό παράδειγμα: ένα μονοδιάστατο πλέγμα με τοπολογικές καταστάσεις γνωστές ως πλέγμα παπιγιόν, το οποίο συνίσταται από ζεύγη ατόμων που είναι τοποθετημένα με αντεστραμμένες θέσεις σε μια σειρά. Έδειξαν ότι η χαμιλτονιανή για αυτό το πλέγμα είναι η τετραγωνική ρίζα της χαμιλτονιανής για ένα (μη-τοπολογικό) πλέγμα ζευγών ατόμων διευθετημένων όπως βήματα σε μια σκάλα. Επεκτείνοντας από αυτή την περίπτωση, οι συγγραφείς προσδιόρισαν γενικά χαρακτηριστικά μιας λειτουργίας τετραγωνικής ρίζας που καταλήγει σε ένα τοπολογικό πλέγμα, τόσο μιας διάστασης, όσο και δυο διαστάσεων.

Πηγή: APS

Περισσότερα στη δημοσίευση: Topological tight-binding models from nontrivial square roots. Physical Review B 95.