- Συνέντευξη: Ο ερευνητής Διονύσης Αντύπας με απλά λόγια μας μαθαίνει το χαλαρόνιο και τη σχέση του με την σκοτεινή ύλη
- ΝΕLIOTA: Το ερευνητικό πρόγραμμα παρακολούθησης εκλάμψεων λόγω προσκρούσεων παραγήινων αστεροειδών και μετεωροειδών στη Σελήνη
- Podcast: Συζήτηση με τον καθηγητή Νικόλαο Στεργιούλα με αφορμή το σημαντικό εύρημα της εργασίας του για τα άστρα νετρονίων
- Podcast: Ο Διονύσης Σιμόπουλος απαντά σε ερωτήματα για το σύμπαν και την έρευνα που σχετίζεται με αυτό
- Άρθρο με αφορμή το Nobel Φυσικής του 2017: Οι βηματισμοί της Επιστήμης και η πορεία προς τον εντοπισμό των βαρυτικών κυμάτων
- Συνέντευξη: Το ελληνικό εκπαιδευτικό σύστημα με τα μάτια ενός νέου ερευνητή όπως ο κ. Μπάμπουλης (Μέρος 3)
- Συνέντευξη: Ο ερευνητής Νανοτεχνολογίας κ. Μπάμπουλης περιγράφει τη δομή των νέων 2D υλικών και τις εφαρμογές τους (Μέρος 2)
- Συνέντευξη: Συζητώντας με τον ερευνητή κ. Παντελή Μπάμπουλη για τα ενδιαφέροντα τεχνητά υλικά, γερμανένιο και πυριτένιο (Μέρος 1)
- podcast: Τι είναι τα Βαρυτικά Κύματα (Συνέντευξη με τον Ερωτόκριτο Κατσαβουνίδη, διευθυντή έρευνας στο ΜΙΤ)
- podcast: Αναζητώντας τα Βαρυτικά Κύματα (Συνέντευξη με τον Χρήστο Τσάγκα, Αναπληρωτή Καθηγητή του ΑΠΘ)
Nobel Φυσικής 2016: Ο ρόλος της τοπολογίας στην κατανόηση των εξωτικών μορφών της ύλης σε δισδιάστατα και μονοδιάστατα υλικά

Στα συστήματα δυο διαστάσεων, όπως τα λεπτά ρευστά φιλμ ή τα μονοστρωματικά υλικά, μπορούν να παρουσιαστούν εκπληκτικά φαινόμενα, όπως ροές υγρών χωρίς τριβές ή μη-συμβατική ηλεκτρική συμπεριφορά, αλλά και τα μονοδιάστατα συστήματα μπορούν να είναι εξίσου ασυνήθιστα. Για να εξηγήσουν αυτά τα φαινόμενα, οι ερευνητές έχουν στραφεί στις δίνες, στις καμπύλες επιφάνειες και σε άλλα «τοπολογικά» αντικείμενα των οποίων οι ιδιότητες είναι σταθερές και ανεξάρτητες από το ειδικό υλικό που εμπλέκεται. Τρεις πρωτοπόροι στην ανάπτυξη τέτοιων μοντέλων – οι David Thouless, Duncan Haldane και Michael Kosterlitz – βραβεύθηκαν αυτή τη χρονιά με το Nobel για τη Φυσική. Τώρα το τοπολογικό πλαίσιο χρησιμοποιείται ευρέως σε προβλεπόμενες και χαρακτηριζόμενες νέες μορφές της ύλης, μερικές από τις οποίες προσφέρουν τις σταθερές καταστάσεις που θα μπορούσαν να αποθηκεύσουν πληροφορίες για ένα κβαντικό υπολογιστή.
Ο ρόλος της τοπολογίας στην φυσική συμπυκνωμένης ύλης καθιερώθηκε στις αρχές της δεκαετίας του 1970, όταν οι θεωρητικοί συζητούσαν για τις φάσεις μετάβασης σε δισδιάστατα (2D) συστήματα. Προηγούμενη εργασία έδειξε ότι οι συμβατικές μεταβάσεις (όπως μεταξύ νερού και πάγου) δεν θα μπορούσαν να συμβούν σε δυο διαστάσεις, όμως ήταν επίσης καθαρό ότι σε τέτοια αντικείμενα, συνέβαιναν ορισμένα είδη απότομων αλλαγών, όπως για παράδειγμα, υγρά φιλμ που παρουσίαζαν υπερρευστότητα κάτω από μια κρίσιμη θερμοκρασία.
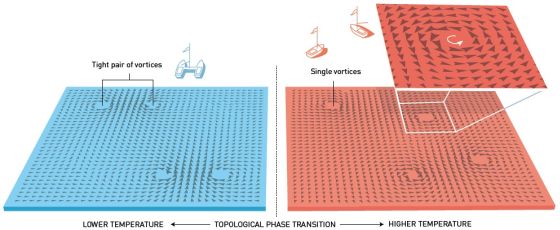
Για να διευθετήσουν την αντιπαράθεση, ο Kosterlitz και ο Thouless φαντάστηκαν μια νέα μορφή της φάσης μετάβασης που βασίζεται στους στροβίλους, στις δίνες, και σε άλλες αποκαλούμενες τοπολογικές ανωμαλίες. Μία δίνη είναι ένα σημείο σε ένα μαγνητικό, για παράδειγμα, φιλμ, γύρω από το οποίο τα μαγνητικά σπιν των ατόμων προσανατολίζονται σε μια κατεύθυνση κατά τη φορά κίνησης των δεικτών του ωρολογίου (προσανατολισμός σε κατεύθυνση αντίθετη από την φορά κίνησης των δεικτών αποκαλείται αντι-δίνη). Αυτό το αντικείμενο μπορεί να είναι αρκετά εύρωστο. «Μόλις διαμορφωθεί μια δίνη είναι πολύ δύσκολο να απαλλαγείς από αυτή», εξηγεί ο Steve Simon από το Πανεπιστήμιο της Οξφόρδης, στο Ηνωμένο Βασίλειο.
Σε υψηλή θερμοκρασία, δίνες και αντι-δίνες είναι πολυάριθμες και τα σπιν είναι ακατάστατα, χαοτικά. Ωστόσο οι Kosterlitz και Thouless, έδειξαν ότι σε χαμηλές θερμοκρασίες, οι δίνες ζευγαρώνουν με αντι-δίνες, μερικώς ακυρώνοντας την επίδρασή τους. Ως αποτέλεσμα, τα σπιν σε όλο το δισδιάστατο υλικό είναι δυνατό σε κάποιο βαθμό να ευθυγραμμίζονται μεταξύ τους. Η ευθυγράμμιση αυτή είναι μια μορφή «τοπολογικής τάξης» που ισχύει γενικότερα σε δισδιάστατα συστήματα ατόμων (ή ηλεκτρονίων) τα οποία ευθυγραμμίζουν μια πλευρά των κβαντικών τους καταστάσεων – τις κβαντομηχανικές τους φάσεις. Ως τέτοια, η μετάβαση Kosterlitz-Thouless (KT) εξηγεί την ανάδυση και της υπερρευστότητας και της υπεραγωγιμότητας σε δυο διαστάσεις.
Μια δεκαετία αργότερα, ο Thouless και οι συνεργάτες του και πάλι στράφηκαν στην τοπολογική επιχειρηματολογία για την εξήγηση του κβαντικού φαινομένου Hall (QHE) που ανακαλύφθηκε το 1980. Το QHE είναι, όπως και το κλασικό φαινόμενο Hall, μια επαγόμενη διαφορά δυναμικού σε ένα ρευματοφόρο αγωγό που βρίσκεται μέσα σε μαγνητικό πεδίο. Στην κβαντική περίπτωση, ωστόσο, ο αγωγός είναι περιορισμένος σε δυο διαστάσεις. Όταν το ρεύμα ρέει κατά μια κατεύθυνση (ας πούμε βορράς – νότος) δια μέσου του αγωγού, μετριέται μια εγκάρσια (ανατολή – δύση) διαφορά δυναμικού. Περιέργως, καθώς το μαγνητικό πεδίο αυξάνεται βαθμιαία, ο λόγος του ρεύματος προς τη διαφορά δυναμικού (αποκαλείται αγωγιμότητα Hall) αυξάνεται με διακριτά άλματα. Οι τιμές είναι ακέραια πολλαπλάσια μιας στοιχειώδους μονάδας αγωγιμότητας. Η κβάντωση αυτή δεν εξαρτάται από τον τύπο του υλικού ή από το εάν περιέχει οποιεσδήποτε ατέλειες ή προσμίξεις. «Θα περιμένατε ότι ρίχνοντας “βρωμιά” μέσα στο σύστημα θα οδηγούσε στην εξαφάνιση του φαινομένου, αλλά αυτό δεν συμβαίνει», είπε ο Marcel den Nijs, από το Πανεπιστήμιο της Ουάσινγκτον και ένας από τους συγγραφείς της εργασίας μαζί με τον Thouless.
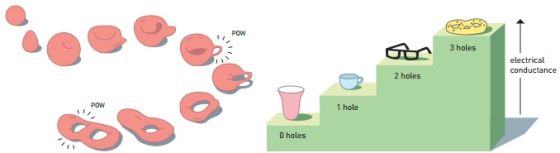
Για να εξηγήσει αυτή την ευρωστία, η ομάδα του Thouless μελέτησε όλες τις κυματοσυναρτήσεις που μπορούν να περιγράψουν ηλεκτρόνια σε δισδιάστατα υλικά και αναπαράστησε αυτό το σύνολο των πιθανοτήτων με μια καμπυλωμένη επιφάνεια. Το σχήμα αυτής της επιφάνειας μπορεί να χαρακτηριστεί από ένα αριθμό, που ονομάζεται τοπολογικό αναλλοίωτο, ο οποίος έχει κάποια σταθερότητα, όπως οι δίνες στην μετάβαση KT. Ένα κοινό παράδειγμα για ένα τοπολογικό αναλλοίωτο είναι ο αριθμός των οπών σε ένα αντικείμενο, όπως ένα ντόνατς ή ένα πρέτσελ. Μπορείς να παραμορφώσεις ένα στρέτσελ λίγο, αλλά ο αριθμός των οπών δεν αλλάζει. Είναι σίγουρο ότι με ορισμένες ενέργειες μπορείς να τρυπήσεις ή να κόψεις το πρέτσελ για να κάνεις περισσότερες ή λιγότερες τρύπες, αλλά οι τρύπες μετράνε πάντα τις αλλαγές με άλματα κατά ένα ακέραιο ποσό (δεν υπάρχουν μισές τρύπες). Ο Thouless και οι συνεργάτες του έδειξαν ότι τα τοπολογικά αναλλοίωτα που παρήγαγαν σχετίζονταν με τους ακεραίους που χαρακτήριζαν τα βήματα αγωγιμότητας Hall. Το αποτέλεσμα αυτό αιτιολογούσε την κβάντωση και επίσης εξηγούσε γιατί το QHE είναι τόσο εύρωστο: μικρές αλλαγές στο υλικό μπορούν να επηρεάσουν το σύνολο των κυματοσυναρτήσεων του ηλεκτρονίου, αλλά το τοπολογικό αναλλοίωτο που περιγράφει το σύνολο είναι πολύ δυσκολότερο να αλλάξει.
Η ιδέα ότι η τοπολογία θα μπορούσε να χρησιμοποιηθεί για να χαρακτηρίσει τη φάση της ύλης χρησιμοποιήθηκε επίσης από τον Haldane στην εργασία του στις αλυσίδες σπιν – μονοδιάστατα συστήματα από συζευγμένα άτομα που διαμορφώνονται σε μαγνητικά υλικά. «Οι εργασίες αυτές ξεκίνησαν μια τάση, που είναι απολύτως κυρίαρχη τώρα, κατά την οποία μπορείς να χαρακτηρίσεις ύλη με τοπολογικό αναλλοίωτο και να μην νοιάζεσαι για τις μικρές λεπτομέρειες», είπε ο Simon. Το πλέον κυρίαρχο παράδειγμα αυτής της τάσης είναι το πεδίο των τοπολογικών μονωτών – υλικά τα οποία άγουν τον ηλεκτρισμό μόνο στην επιφάνειά τους. Αυτά τα ρεύματα επιφάνειας περιγράφονται ως «προστατευμένα» με την τοπολογία από ατέλειες κατά μήκος της επιφάνειας, που κανονικά θα ανάγκαζε τα ηλεκτρόνια να διασκορπίζονται. Η ευρωστία που παρουσιάζεται θα μπορούσε να κάνει τα υλικά αυτά ωφέλημα, ως πολύ αποδοτικά νανοσύρματα ή ως η σταθερή βάση αποθήκευσης σε έναν κβαντικό υπολογιστή, είπε ο den Nijs.
Πηγή: APS
Περισσότερα στις δημοσιεύσεις (είναι αυτή την περίοδο ελεύθερα):
(1) Long Range Order and Metastability in Two Dimensional Solids and Superfluids. (Application of Dislocation Theory). Journal of Physics C: Solid State Physics, Volume 5, Number 11
(2) Ordering, Metastability and Phase Transitions in Two-Dimensional Systems. Journal of Physics C: Solid State Physics, Volume 6, Number 7
(3) Βραβείο Nobel 2016 στη Φυσική: Επειδή ανακάλυψαν τα μυστικά της εξωτικής ύλης. Egno.gr, όπου υπάρχουν και άλλα άρθρα σχετικά με το θέμα.