Μαθηματικοί κάνουν μια σημαντική ανακάλυψη για τους Πρώτους Αριθμούς

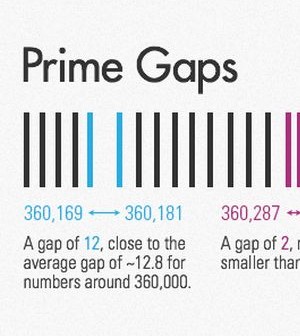
Τον Μάιο του 2013, ο μαθηματικός Yitang Zhang από το Πανεπιστήμιο του New Hampsire έκανε το πρώτο βήμα στην επίλυση ενός από τα διασημότερα ανοικτά προβλήματα στην ιστορία των μαθηματικών, την περίφημη εικασία των Διδύμων Πρώτων.

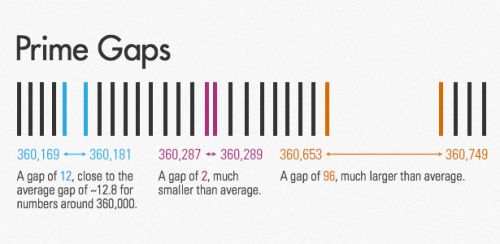
Δίδυμοι πρώτοι ονομάζονται οι πρώτοι αριθμοί που η διαφορά τους είναι 2. Για παράδειγμα, οι αριθμοί 11 και 13, 17 και 19 και 2549, 2551 είναι δίδυμοι πρώτοι αριθμοί. Για να βρεθεί λύση στην εικασία των Διδύμων Πρώτων θα πρέπει να αποδειχτεί πως υπάρχουν άπειροι πρώτοι p τέτοιοι ώστε και ο αριθμός p + 2 να είναι πρώτος.

Σημειώνεται ότι 2 είναι η μικρότερη απόσταση μεταξύ δύο πρώτων, καθώς αν ο p είναι πρώτος τότε θα είναι περιττός (με μοναδική εξαίρεση τον αριθμό 2) και άρα ο p+1 θα είναι άρτιος και άρα σύνθετος αριθμός. Το πρόβλημα των Διδύμων Πρώτων εικάζει ότι υπάρχουν άπειρα τέτοια ζεύγη, αλλά κανείς μέχρι σήμερα δεν ήταν σε θέση να το αποδείξει.

Το 2005 μια ομάδα μαθηματικών έδειξε ότι ο αριθμός των πρώτων ζευγών με διαφορά 16 μονάδες είναι άπειρος. Το πρόβλημα, όμως, ήταν ότι η απόδειξή τους βασίστηκε σε μια άλλη αναπόδεικτη εικασία. Ο μαθηματικός Υ. Ζhang, από το Πανεπιστήμιο του New Hampshire απέδειξε, πρώτη φορά, ότι ο αριθμός των ζευγών των πρώτων αριθμών με διαφορά 70 εκατομμύρια μονάδες είναι άπειρος.

Τώρα οι μαθηματικοί έχουν κάνει την πρώτη ουσιαστική πρόοδο, ύστερα από 76 χρόνια, στην επίλυση του αντίστροφου προβλήματος : Πόσο μπορεί να απέχουν μεταξύ τους οι διαδοχικοί πρώτοι αριθμοί ; H μέση απόσταση ανάμεσα σε δύο διαδοχικούς πρώτους τείνει στο άπειρο καθώς αυξάνονται, αλλά σε κάθε πεπερασμένο κατάλογο αριθμών, το μέγιστο χάσμα μεταξύ δυο πρώτων αριθμών θα μπορούσε να είναι μεγαλύτερο από το μέσο όρο. Κανείς δεν ήταν σε θέση να ορίσει πόσο μεγάλο θα μπορούσε να είναι αυτό το χάσμα ανάμεσα στους αριθμούς.

Ο Paul Erdős, αριστερά, και ο Terence Tao συζητώντας μαθηματικά το 1985. Τον περασμένο Αύγουστο ο Tao και τέσσερις άλλοι μαθηματικοί απέδειξαν μια παλιά εικασία του Erdős σηματοδοτώντας την πρώτη σημαντική πρόοδο, σε 76 χρόνια, στην κατανόηση σχετικά με το εύρος του χάσματος ανάμεσα στους πρώτους αριθμούς.

Τον περασμένο Αύγουστο, δύο διαφορετικές ομάδες μαθηματικών δημοσιοποίησαν τις εργασίες τους στις οποίες αποδεικνύουν την περίφημη Εικασία του διάσημου μαθηματικού Paul Erdős, σχετικά με το εύρος του χάσματος ανάμεσα στους πρώτους αριθμούς. Οι δύο ομάδες συνεργάζονται ήδη στενά, για να ενδυναμώσουν τα αποτελέσματα που αφορούν τη διεύρυνση της απόστασης των πρώτων αριθμών και να ανακοινώσουν, σύντομα, τα συμπεράσματά τους.

Πηγή: http://thalesandfriends.org/

Πλήρες το άρθρο: https://www.quantamagazine.org/20141210-prime-gap-grows-after-decades-long-lull/