Ερευνητές παρατήρησαν ένα κρίσιμο σημείο στην ηλεκτρική δραστηριότητα του εγκεφάλου

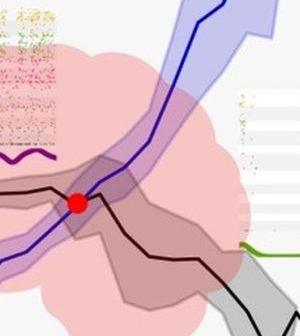
Ερευνητές παρατήρησαν ένα κρίσιμο σημείο – ένα χαρακτηριστικό ενδεικτικό μιας συνεχούς φάσης μετάβασης – στην ηλεκτρική δραστηριότητα του εγκεφάλου καθώς αλλάζει από μια αδρανή κατάσταση ύπνωσης σε μια κατάσταση αφύπνισης.

Κάθε πρωί, οι εγκέφαλοί μας μεταβαίνουν από το να είναι σε βαθειά ύπνωση στο να υπάρχουν σε εγρήγορση και ξύπνιοι. Οι ερευνητές θεωρούν ότι αυτή η μετάβαση είναι συνεχής, πράγμα που σημαίνει ότι σημαδεύεται από μια κατάσταση μετάβασης με μοναδικές ιδιότητες, που ονομάζεται κρίσιμο σημείο, όμως τα δεδομένα παραμένουν αμφισβητήσιμα. Ο Antonio Fontenele στο Ομοσπονδιακό Πανεπιστήμιο του Pernambuco, στη Βραζιλία και οι συνάδελφοί του αναφέρουν τώρα νέα δεδομένα που προσθέτουν βάρος στο επιχείρημα του «κρίσιμου εγκεφάλου». Σε πειράματα, βρήκαν ότι εγκέφαλοι αρουραίων περνούν ένα κρίσιμο σημείο καθώς οι εγκέφαλοι αλλάζουν μεταξύ καταστάσεων με διαφορετικά είδη νευρωνικής συμπεριφοράς. Τα αποτελέσματα της ομάδας θα μπορούσαν να βοηθήσουν να περιοριστούν οι μηχανισμοί οι οποίοι υποστηρίζουν το κρίσιμο σημείο του εγκεφάλου.

Οι νευρώνες εκπέμπουν πολύ μικρές αιχμές τάσης, είτε σύγχρονα καθώς επαναλαμβάνονται οι ωθήσεις ή ασύγχρονα ως ένα σταθερό σήμα σαν θόρυβος. Προηγούμενη εργασία έχει δείξει ότι οι σύγχρονες αιχμές (κορυφώσεις) συμβαίνουν σε ζώα που κοιμούνται και οι ασύγχρονες σε αυτά που είναι ξύπνια. Έτσι, για να μελετήσουν τη μετάβαση μεταξύ των δυο αυτών καταστάσεων, ο Fontenele και οι συνεργάτες του κοίταξαν στην δραστηριότητα κορύφωσης στον πρωτεύοντα οπτικό φλοιό αναισθητοποιημένων αρουραίων, συσσωρεύοντας ένα μεγάλο σύνολο δεδομένων με ένα ευρύ φάσμα καθεστώτων κορύφωσης.

Τα δεδομένα τους αποκαλύπτουν «χιονοστιβάδες» κορύφωσης – κορυφώσεις που συμβαίνουν σε ταχείες αλληλουχίες, από τις οποίες προηγούνται και οι οποίες ακολουθούνται από σιωπή. Ο αριθμός των κορυφώσεων σε κάθε χιονοστιβάδα προσδιόριζε το «μέγεθος» και η διάρκεια της κάθε χιονοστιβάδα προσδιόριζαν τη «διάρκεια ζωής». Καθώς οι εγκέφαλοι των αρουραίων πήγαιναν από μια σύγχρονη σε μια ασύγχρονη κατάσταση, η ομάδα βρήκε ότι οι κατανομές του μεγέθους και της διάρκειας ζωής της χιονοστιβάδας ακολουθούσαν νόμους ισχύος, σηματοδοτώντας το αποκαλούμενο αναλλοίωτο κλίμακας [1] – μια κλασική υπογραφή ενός κρίσιμου σημείου. Επιπλέον, οι εκθέτες των παρατηρούμενων νόμων ισχύος διαφέρουν από αυτούς που βρέθηκαν σε προηγούμενα πειράματα, δείχνοντας ότι η φάση μετάβασης ανήκει σε μια άλλη «τάξη καθολικότητας». Οι ερευνητές, ωστόσο, δεν γνωρίζουν ακόμη τι μπορεί να είναι αυτή η τάξη.

Πηγή: American Physical Society

Περισσότερα στη δημοσίευση: Criticality between Cortical States. Physical Review Letters.

[1] Σημείωση egno.gr: Στη φυσική, τα μαθητικά και στη στατιστική, αναλλοίωτο κλίμακας (scale invariance) είναι ένα χαρακτηριστικό αντικειμένων ή νόμων που δεν αλλάζει εάν οι κλίμακες μήκους, ενέργειας ή άλλων μεταβλητών, πολλαπλασιάζονται με έναν κοινό παράγοντα, έτσι αντιπροσωπεύουν μια καθολικότητα.