- Συνέντευξη: Ο ερευνητής Διονύσης Αντύπας με απλά λόγια μας μαθαίνει το χαλαρόνιο και τη σχέση του με την σκοτεινή ύλη
- ΝΕLIOTA: Το ερευνητικό πρόγραμμα παρακολούθησης εκλάμψεων λόγω προσκρούσεων παραγήινων αστεροειδών και μετεωροειδών στη Σελήνη
- Podcast: Συζήτηση με τον καθηγητή Νικόλαο Στεργιούλα με αφορμή το σημαντικό εύρημα της εργασίας του για τα άστρα νετρονίων
- Podcast: Ο Διονύσης Σιμόπουλος απαντά σε ερωτήματα για το σύμπαν και την έρευνα που σχετίζεται με αυτό
- Άρθρο με αφορμή το Nobel Φυσικής του 2017: Οι βηματισμοί της Επιστήμης και η πορεία προς τον εντοπισμό των βαρυτικών κυμάτων
- Συνέντευξη: Το ελληνικό εκπαιδευτικό σύστημα με τα μάτια ενός νέου ερευνητή όπως ο κ. Μπάμπουλης (Μέρος 3)
- Συνέντευξη: Ο ερευνητής Νανοτεχνολογίας κ. Μπάμπουλης περιγράφει τη δομή των νέων 2D υλικών και τις εφαρμογές τους (Μέρος 2)
- Συνέντευξη: Συζητώντας με τον ερευνητή κ. Παντελή Μπάμπουλη για τα ενδιαφέροντα τεχνητά υλικά, γερμανένιο και πυριτένιο (Μέρος 1)
- podcast: Τι είναι τα Βαρυτικά Κύματα (Συνέντευξη με τον Ερωτόκριτο Κατσαβουνίδη, διευθυντή έρευνας στο ΜΙΤ)
- podcast: Αναζητώντας τα Βαρυτικά Κύματα (Συνέντευξη με τον Χρήστο Τσάγκα, Αναπληρωτή Καθηγητή του ΑΠΘ)
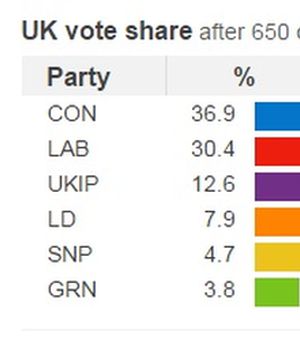
Πρέπει ένα πολιτικό κόμμα να σχηματίσει ένα συνασπισμό; Για να αποφασίσει χρειάζονται τα μαθηματικά (άντε και οι ψηφοφόροι)

Οι μαθηματικές ιδέες και τα εργαλεία χρησιμοποιούνται συχνά για να περιγράψουν πτυχές των μεγάλων μακροσκοπικών συστημάτων. Τα παραδείγματα αφθονούν σε ποικίλους τομείς, όπως από την οικονομία μέχρι την ψυχολογία. Σε μια μελέτη που δημοσιεύθηκε τον περασμένο μήνα στην SIAM Journal on Applied Mathematics, ο συγγραφέας Fabio Bagarello καθηγητής Μαθηματικής Φυσικής στο Πανεπιστήμιο του Παλέρμο, στην Ιταλία, προτείνει μαθηματικά μοντέλα για να αναλύσουν τη λήψη πολιτικών αποφάσεων. Χρησιμοποιώντας μια δυναμική προσέγγιση η οποία ενσωματώνει τις αλληλεπιδράσεις μεταξύ των πολιτικών κομμάτων και των συστατικών τους, το μοντέλο προσπαθεί να συνάγει αν τα κόμματα θα πρέπει να σχηματίζουν συνασπισμούς κάτω από διάφορες συνθήκες.
«Τα μαθηματικά είναι σημαντικά σε πολλές πτυχές της κοινωνικής συμπεριφοράς. Η πολιτική είναι μόνο μία από αυτές τις πτυχές, δεδομένου ότι μερικές από τις τυπικές συμπεριφορές στην πολιτική μπορεί να χαρακτηρίζονται από κατάλληλες ποσότητες οι οποίες, συνήθως, εξελίσσονται στο χρόνο», λέει ο Bagarello. «Με άλλα λόγια, τα πολιτικά κόμματα αποτελούν παραδείγματα δυναμικών συστημάτων».
Ο Bagarello χρησιμοποιεί μια Χαμιλτονιανή, έναν τελεστή ο οποίος μπορεί να περιγράφει τις αλληλεπιδράσεις μεταξύ των διαφόρων συστατικών ενός συστήματος. Στο μοντέλο, που χρησιμοποίησε, εξετάστηκαν τρία κόμματα σε ένα σύστημα. Κάθε κόμμα μπορεί να κάνει μία από τις δύο επιλογές: να σχηματίσει συνασπισμό ή όχι. Αυτό οδηγεί σε οκτώ διαφορετικές δυνατότητες που μπορεί να αλλάξουν με την πάροδο του χρόνου. Έπειτα καθορίστηκε η χρονική συμπεριφορά των «συναρτήσεων απόφασης» των πολιτικών κομμάτων, που περιγράφει την πιθανότητα ενός κόμματος να σχηματίσει ένα συνασπισμό. Για να πάρουν αποφάσεις, τα κόμματα πρέπει να αλληλεπιδράσουν με τους ψηφοφόρους ή τους εκλογείς. Η αλληλεπίδραση αυτή είναι αποφασιστικής σημασίας για τις τελικές αποφάσεις τους και το μοντέλο τις λαμβάνει υπόψη μέσω ενός ανοικτού συστήματος, το οποίο υπολογίζει την αλληλεπίδραση των ψηφοφόρων.
«Αρκετά συχνά, αυτά τα είδη των δυναμικών συστημάτων περιγράφονται από διαφορικές εξισώσεις των οποίων οι διαφορετικοί όροι περιγράφουν διαφορετικά φαινόμενα. Στην προσέγγισή μου το κύριο συστατικό δεν είναι η διαφορική εξίσωση, αλλά μια Χαμιλτονιανή-τελεστής από την οποία μπορεί να συναχθεί η δυναμική κάποιων σχετικών «παρατηρήσιμων» του συστήματος », εξηγεί ο Bagarello. «Αυτό αφήνει έναν εύκολο τρόπο να διαμορφωθεί ένα «ανοικτό σύστημα», στο οποίο λίγοι παράγοντες (τα κόμματα) αλληλεπιδρούν με πολλούς (τους ψηφοφόρους) και μπορούμε να δείξουμε πώς οι ψηφοφόροι κατευθύνουν τη συμπεριφορά των διαφόρων κομμάτων».
«Αναλύθηκαν αρκετά μακροσκοπικά συστήματα, με τη χρήση τέτοιων τελεστικών τεχνικών. Έχω υιοθετήσει το ίδιο γενικό πλαίσιο στην περιγραφή των «ερωτικών σχέσεων», των μεταναστεύσεων, κλειστών οικολογικών συστημάτων και απλοποιημένων χρηματιστηριακών αγορών», συνέχισε ο Bagarello. «Η ενασχόληση με τα χρηματιστήρια ήταν το αρχικό ενδιαφέρον μου, που οφείλεται στο γεγονός ότι οι επιχειρηματίες ανταλλάσσουν διακριτές ποσότητες που περιγράφονται καλά από απλούς και γνωστούς αλγεβρικούς κανόνες».
Οι μελλοντικές κατευθύνσεις στην έρευνα μπορεί να επιτρέψουν στα κόμματα, όχι μόνο για να προσδιορίσει αν θα πρέπει να σχηματίσουν μια συμμαχία ή όχι, αλλά επίσης να προτείνουν ποια κόμματα να σχηματίσουν συμμαχίες με ποια. «Αυτό είναι μέρος μιας πιθανής εκτεταμένη έκδοσης του μοντέλου και το έργο βρίσκεται σε εξέλιξη», λέει ο Bagarello. «Το μοντέλο αυτό θα μπορούσε επίσης να βελτιωθεί με την προσθήκη ορισμένων μη γραμμικοτήτων στους όρους αλληλεπίδρασης. Αυτές θα μπορούσαν να χρησιμοποιηθούν, για παράδειγμα, για να παραχθεί ένα πιο εκλεπτυσμένο μοντέλο στο οποίο οι συμπεριφορές των κομμάτων να οδηγούνται σε σημαντικό βαθμό από τις αποφάσεις των άλλων κομμάτων».
Πηγή: Society for Industrial and Applied Mathematics
Περισσότερα στο άρθρο: Fabio Bagarello, An Operator View on Alliances in Politics, SIAM J. Appl. Math., 75(2), 564–584. (21 pages)